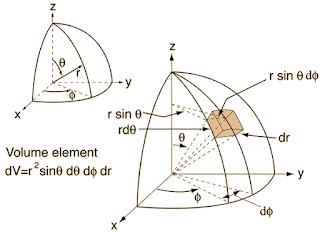
Because astronomy works on the Celestial Sphere, spherical coordinates play a very important role in astronomy. Most of the time we can ignore the intricacies of physics in 3-dimensions and work in a 2D far-field regime. (The far-field regime is just fancy speak for "small-angles"). However, it can be useful to understand why spherical coordinates are they way they are. Here, we will quickly derive the spherical differential volume element. Differential, just means vanishingly small. To let the cat out of the bag, the spherical differential volume element is, \[ dV = r^2 \sin{\theta}\, dr\, d\theta \, d\phi .\] The figure above shows the coordinate system we will be working with. This form is commonly used in astronomy, and also in some physics. However, it is different from the way mathematicians define it. In mathematics the \(\theta\) and the \(\phi\) are often switched. The astronomy convention is the more commonly used one in physics and astronomy (sorry mathematica...