A Quick Look at Spherical Coordinates


Because astronomy works on the Celestial Sphere, spherical coordinates play a very important role in astronomy. Most of the time we can ignore the intricacies of physics in 3-dimensions and work in a 2D far-field regime. (The far-field regime is just fancy speak for "small-angles"). However, it can be useful to understand why spherical coordinates are they way they are. Here, we will quickly derive the spherical differential volume element. Differential, just means vanishingly small. To let the cat out of the bag, the spherical differential volume element is,
\[ dV = r^2 \sin{\theta}\, dr\, d\theta \, d\phi .\]


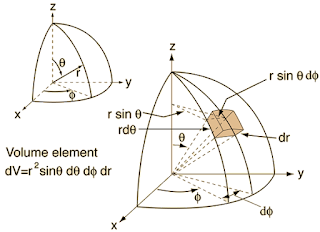
The figure above shows the coordinate system we will be working with. This form is commonly used in astronomy, and also in some physics. However, it is different from the way mathematicians define it. In mathematics the \(\theta\) and the \(\phi\) are often switched. The astronomy convention is the more commonly used one in physics and astronomy (sorry mathematical physicists). Moving on.

Initially, we would be inclined to say that a differential box with sides of \((dr,\, d\theta,\, d\phi)\) would have a volume \(dV = dr\, d\theta \, d\phi\). Immediately we should realize this is wrong because the units are incorrect. The units of volume are \(L^3\) not \(L\times (angle)^2\). The being spherical, we must use the arc lengths of the sides, not just the angular lengths. For an arc, the arc length is \(s = r\theta\), where \(\theta\) is the angle subtended by an arc on a circle of radius \(r\). So what circles are our angle on?

The \(\theta\) coordinate measures the angle along great circles (the intersection of the surface of a sphere and a plane that passes through the center, i.e. circles that pass through the poles, like meridians). In other words, \(\theta\) measures the polar or zenith angle. The \(\phi\) coordinate measures angle along a circle placed at \(\theta\) from the zenith. The circle is the intersection of a cone with opening angle \(\theta\), starting at the origin, intersecting the sphere. Note that the radius of this circle will not necessarily be the radius of the sphere.

Now that we have defined which circles are relevant to which angles, we can determine the arc length. For \(d\theta\), the radius of the circle it lies on is always \(r\) because it is a great circle. For $d\phi$ the circle radius will depend on \(\theta\), specifically, if we examine the diagram, \(r \sin{\theta}\), because it is the distance to the z-axis, not the origin, that matters. This makes sense particularly if we notice how the lines of constant \(d\phi\) get closer as \(\theta \rightarrow 0\). Therefore, the area of that patch is
\[dA = r\, d\theta \times r\, d\phi,\]
and the volume is just \(dr \, dA\).





Comments

Post a Comment

Popular posts from this blog

Coding and the Interwebs

Image
If there is one thing you should know about learning to code, it is that the internet is your friend . Learning how to find what you need on the internet is an important skill to learn. A lot of the skill comes with time, but there are a few things that can get you going. Someone has had the same problem you are having. There is an answer. Stack Overflow and Stack Exchange are miracles of the internet. Don't worry which is which unless you want to Occam's Razor - Try the simplest solution first, but avoid hackey solutions. How to ask a good question* A good format to follow for asking Google a question is language what you want to do Say I am working on some C++ code, and I want to read in columns from a file. Suppose these have multiple data types, some are strings while others are integers. Example: Alice 1 10 1e3 Bob 2 12 2e3 I would ask C++ how do I read in columns with multiple data types from a file . While this is doable, a Google search sh...
Keep reading

Astrobites

Image
Astrobites is an astro-ph digest developed by Harvard graduates students which now has an international author roll. What is astrobites ? In their own words, Astrobites is a daily astrophysical literature journal written by graduate students in astronomy. Our goal is to present one interesting paper per day in a brief format that is accessible to undergraduate students in the physical sciences who are interested in active research. Essentially, Astrobites takes new research in astronomy and astrophysics and digests it into something approachable. With posts written by graduate students from around the globe, it provides an excellent introduction to technical writing that is understandable for the lay person, yet still scientifically interesting to the expert. Check out some of the posts by the following authors: John Johnson Ben Cook Ben Montet Elisabeth Newton (co-founder) Chris Feasi (co-founder)
Keep reading